Financial Interest Calculations

Financial Interest Calculators offer flexible methods for money and interest loans, mortgages and savings.
The Financial Compound Interest Calculator explained on this page combines flexibility, ease of usage with powerful calculations.

• The calculation is based on 5 main variables ( N, I, PV, PMT and FV).
• Given 4 of the variables the remaining can be calculated.
• Two additional variables make the calculator more flexible, the Period ( P) and After/Before ( B) payment.

Introduction

• If you are not familiar with Financial Calculations please read the Detailed examples chapter first.
• the Mechanism chapter explains the relation of the variables and their meaning.
• the Main Vars chapter explains in detail all main fields of the Finance Interest Calculation Website.
• the Additional chapter explains all additional fields.

Mechanism

A few agreements are used to enter the correct values to the variables. Type operation Agreement Applies to Example Desctiption for Input Calculator. Payments Are always negative. Do not use a valuta-sign. PV, PMT, FV To enter a payment of €100,= use -100. Revenues Are always positive. Do not use a valuta-sign. PV, PMT, FV To enter a revenue of €250,10 use 250.10. Durations Are always positive N To enter a duration of 10½ years use 10.5. Interest Are always positive and in percentages and year-based. I To enter 3.25% per year use 3.25.

Main Vars

Duration - N

The duration is measured in years. To make Period Payments possible during parts of the year use the Period - P settings to select the period. The duration can not be negative. The column Duration contains in the 2nd row the input field for the duration value in years. The 3rd column contains the calculated duration in days.

Example 1 Example 2 In case of a mortgage with a duration of 30 years, input 30 (N = 30). The row below contains the calculated duration in days (i.e. Duration is 30 years meaning 30 x 365 = 10,950 days). In case of a loan with a duration of 2½ years, input 2.25 (N = 2.25). The row below contains the calculated duration in days (i.e. Duration 2¼ years mening 2.25 x 365 = 821 days).

Interest - I

The Interest is always given as a percentage per Year. The column Interest contains in the 2nd row the input field for the interest value. The 3rd row contains the Interest calculated as rate per Period. The interest can not be negative nor can it be greater than 75 %.

Example 1 Example 2 In case of a mortgage interest percentage of 1.79% per year, input 1.79 (I = 1.79). If a monthly period (See the Period column) has been chosen, the 3rd row will calculate a monthly interest of 0.1500%. In case of a loan interest percentage of 1.79% per year, input 1.79 (I = 1.79). If a ½-year period (See the Period column, choose half-year) has been chosen, the 3rd row will calculate a monthly interest of 0.8910%.

Present Values - PV

The Present Value is the current or now value. Do not use valuta-sign and use a decimal point as separator. Comma fields-separators are not allowed.

Example 1 Example 2 In case of a mortgage of €250,000.00, input 250000 PV = 250000). In case of a initial payment for a saving account of €50,000.00, input -50000 (PV = -50000)

Period Payment - PMT

The Period Payment is the amount of money which is received (positive value) or payed (negative value). The number of revenues/payments per year depends on the chosen value of Period - P. The 3rd row in the Period Payment is the indication of the interest payment (revenue (+) or debt(-)) for the chosen Period. Image 2 - Example Interest rate calculation and 1st-Interest payment.

Example 1 For a mortgage of € 250,000.00 a monthly periodical payments of € € 921.50 is required, input -921.50 (PMT= -921.50). Suppose for an annuity the chosen values are as shown in image 2 (P= Month, B=After, N=30, I= to be calculated, PV=-250000, PMT=921.50, FV=0) the calculated value for interest will be 2.00% per year (0.1700% per month) and the 1st Periodical Payment has an interest part of 416.67. Please note: the Interest Payment value of 416.67 is only valid for the 1st payment.

Future Value - FV

The Future Value is the payment which is received (positive value) or payed (negative value) at the end of the total duration of the loan/mortgage/annuity.

Example 1 Example 2 In case of a lineair annuity or mortgage the end-value will be zero (0) input 0. In a saving account the target capital is € 200,000.00, input 200000.

Additional

Period - P

The Period chosen here is used for creating multiple Period Payments per year (PMT). Valid options are Half-year, Quearter, Month, Week and Day.
Example: In case of a mortgage normally the period is a month.

After/Before - B

The value before after in combination with the Period P is used to indicate payment before or after the chosen period.
Example: In case of a mortgage the normal value is after.
Example: In case of a saving account the normal value may be before.

Detailed examples

The detailed examples in this chapter are in a sequential order. So the user has to start with the first Calculate Interest Percentage and follow the other examples from there. This process will make the user familiar with the simple powerful method to calculate complex financial calculation for all kind of common day to day questions on buying, lending, mortgage and saving accounts.

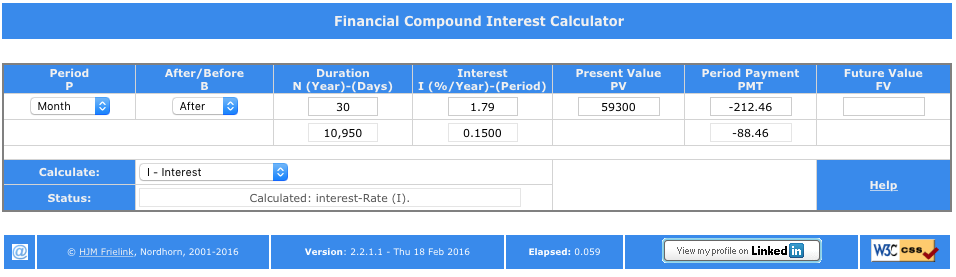
Calculate Interest Percentage

Image-3: InterestRate calculation

Example questions: "What is the interest rate I need to pay to get the money now?
Example answer: Buying a house with a mortgage of € 250,000.- (PV = 250000), a End-Monthly (B= After, P = Month) Period Payment of €1,000.- (PMT = -1000) and a duration of 30 Year (N = 30) the Interest will be 2.6245% per year.
Steps:

1. Set the Calculate combobox to No Calculation. This is the default value so you may not have to change anything.
2. Set the Period combobox to Month.
3. Set the After/Before combobox to After. This is the default value so you may not have to change anything.
4. Set the Duration to 30.
   • The 3rd row of the Duration will indicate 10,950, which is the number of days in 30 years (based on 365 days in a year, without leap years correction).
5. Set the Present Value to 250000.
6. Set the Period Payment to -1000.
7. Set the Future Value to 0. This is the default value so you may not have to change anything.
8. Set the Calculate combobox to i-Interest.
   • The calculation will be initialized and the result will be shown very shortly.
   • In the 3rd row of the Period Payment column -545.83. This is the Interest-Payment-Value for the Interest in the 1st payment. See the Mechanism part for full details.
   • In the 2nd row of the Interest column 2.62. This the percentage of the interest per Year 2.62%.
   • In the 3rd row of the Interest column 0.2200. This is the percentage of the interest per Month (the chosen period) 0.2200%.
   • In the row Status the text: Calculated: Interest-Rate (I).

In case of Status field shows Iteration calculation error. Reached maximum number of iterations! you have made an error in filling the correct values. Review your Website Screen with image 3.

Period Payment Calculation

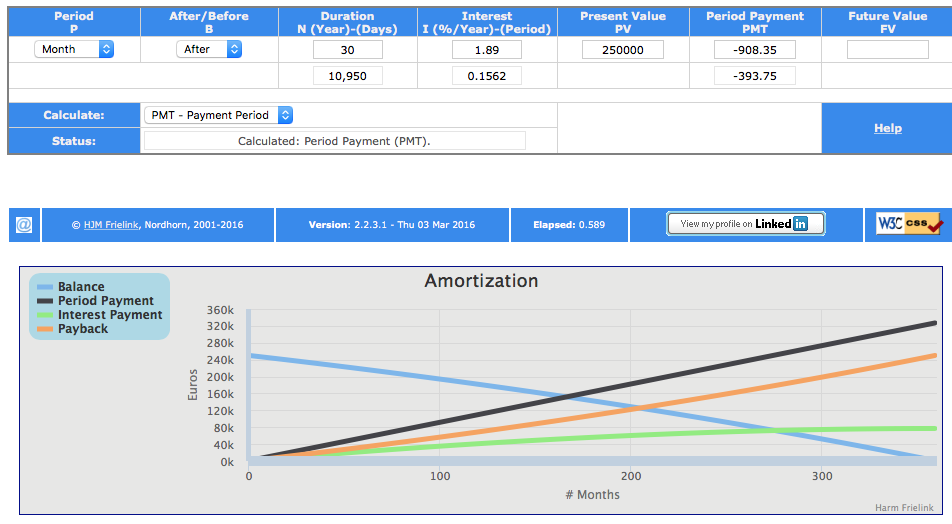
See the example above, but now with an Interest of 3% will yield to an Period Payment of €1,048.56 (-1048.56).
Steps:

• Set the Calculate combobox to PMT - Payment Period.
  1. The value in the Period Payment may be changed to -999.42, because the values on the screen are rounded and the value for the PMT is instantly recalculated.
• Set the Interest to 3. Accept the entry with the tab-key or the Enter-key.
  1. The value for the PMT changes to -1,048.56.
  2. The value for the 3rd row under the column PMT (=1st Interest Payment) changes to -625.

Future Value Calculation

Suppose you did not use the payment for a mortgage but use it for a saving account.
Step:

• Do not change
  1. After/Before B = A
  2. Duration N = 30
  3. Interest I = 3
  4. Period Payment PMT = -1048.56
• Change:
  • 1. Set Calculate to No Calculation. This prevents that the calculation overwrites the value for the Period Payment.
  1. Set PV to 0.
  2. Set Calculate to FV -Future Value will yield € 606,815.34 (606815.34).

What does this mean?

• You bought a house for € 250,000.00 and paid € 1,048.56 monthly over 30 years.
• When you saved the € 1,048.56 monthly over 30 years you have earned over € 600,000.00.

Is that for real. Yes, but the Bank will never pay the same Interest for borrowing and saving!

Help

The calculator is written in PHP and JavaScript using jQuery AJAX implementation. A previous version worked with Java and a JavaApplet.

Graph support

The amortization graph is only shown when you make a calculation for a period payment. An example is shown when you click on the following link https://www.harmfrielink.nl/Finance/FinCalc.php?test.
The above image shows the screen when you click on the link.

What is Amortization?

Webster's dictionary defines amortization as, "the systematic repayment of a debt". The emphasis is on the word systematic. Amortizing a loan means paying it down, bit by bit.

Usually this means making regular monthly payments, and this is what is done for mortgage, for example. But any periodic payment over time to a loan is amortization.

The great advantage of amortization is that you know how much you have to pay each month, under a fixed interest rate, to finish paying off the loan at a specific time. You can work out an amortization table to show each payment.

Graph Amortization

In the graph you see the Balance (the remaining value of the loan in time), the sum of the Period Payments, the sum of the Interest payments and the sum of the payback. If you click on the name of the items in the Legenda you can toggle the lines in the graph. If you hoover over the line you see the data.

See also

• Financial Interest Calculator by Harm Frielink
• Pensioen, Intrawiki Pensioen van HaFr, not accessible for anybody else.